【CEDC】Online Collaborative Data Caching in Edge Computing
要解决的问题:collaborative edge data caching (CEDC) problem
在满足边缘计算环境中的约束条件(如服务器容量、性能约束)的前提下,最小化包括数据缓存成本、数据迁移成本和服务质量(QoS)惩罚在内的系统成本
本文的主要贡献:
- 从应用供应商的角度对 CEDC 问题进行了建模和公式化,并证明了它是NP-complete 问题
- 我们基于 Lyapunov 优化 提出了一个在线算法 CEDC-O,来解决 CEDC 问题,并证明了它具有可证明的近似最优性能。
- 在一个真实世界的数据集上评估了我们算法的性能
论文结构:将问题代数化 → 提出算法 → 评估算法(理论+实验)
就是单纯的 Lyapunov 优化
- 边缘服务器的计算和存储资源是有限的(server capacity constraint)
- 边缘服务器只能覆盖一定的区域 (server coverage constraint)
- 用户和边缘服务器都可以向附近的其他边缘服务器求援 (server adjacency constraint)
System Model
System Architecture
Data Retrieval Latency
System Cost = Data Caching Cost + Data Migration Cost + QoS(quality-of-service) Penalty
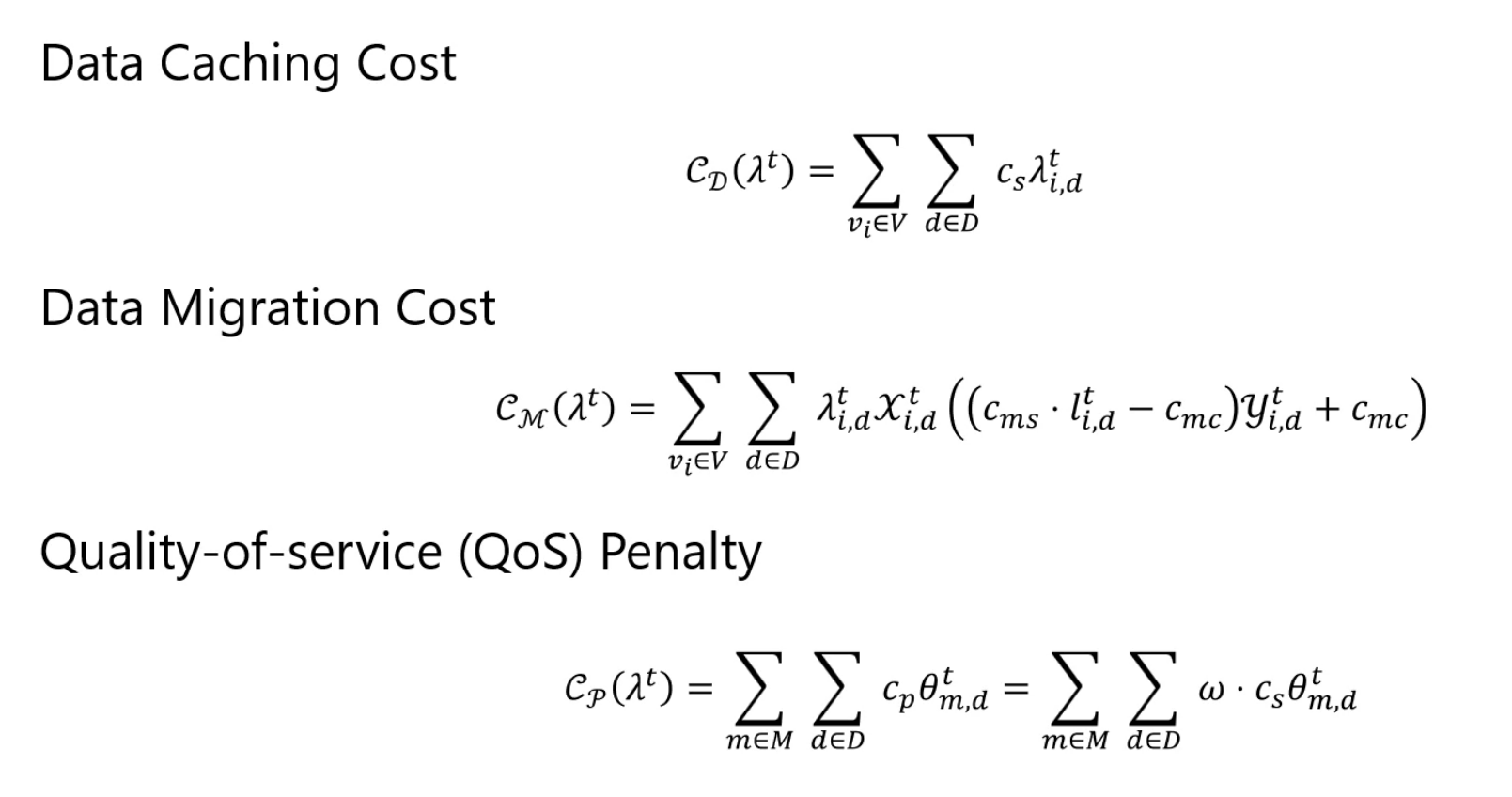
Data Migration Cost
如果一个用户在覆盖他的边缘中没有找到所需要的 数据,可以让边缘服务器在周围的边缘服务器上寻找。Data Migration Cost 会比较从云端拉取数据和从周围的边缘服务器拉取数据所耗费的时间,选择省时间的那个。
因此,
因为:
所以当
当
QoS Penalty
大部分情况下等价于从云端获取数据的开销。
While pursing this optimization objective, it is also necessary to stabilize the time-averaged system latency perceived by the users in the long term.
在最小化 system loss 的同时,也需要保持按时间平均的系统延时的稳定,也就是需要满足:
在边缘计算环境中,数据请求具有非常高的随机性。所以,系统的长期表现比短期表现更重要。因此,CEDC 问题可描述为下面的约束优化问题:
Online Algorithm CEDC-O
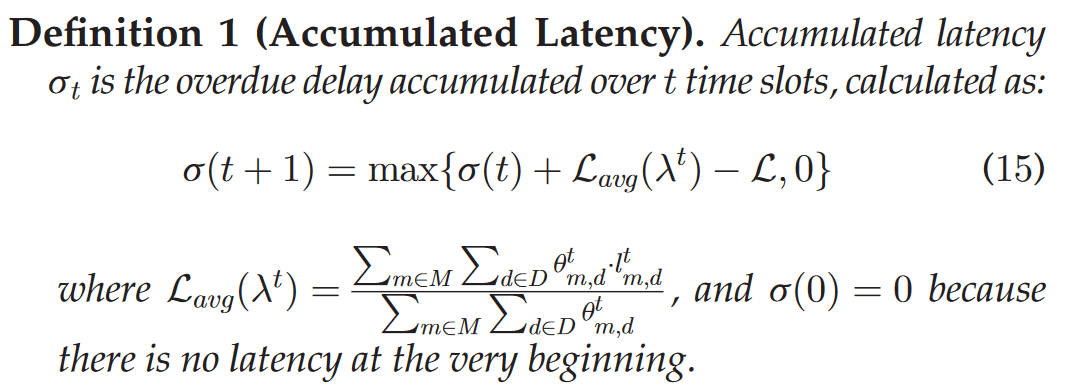

得到了 Lyapunov drift 的上限后,定义 drift-plus-penalty 函数
其中
显然有:
在每一轮中都需要在保持系统稳定的情况下最小化 cost 函数
所以约束优化问题

CEDC-O 算法只需要当前时刻的 data requests 来优化
观察式子 (20),CEDC-O 利用 Lyapunov 优化 在目标函数
Perfomance Analysis
理论证明
- 定理3:CEDC-O 算法按时间平均的 system cost 是
级别的——证明没看懂 - 假设最优化问题
的解是 ,并且对应的 system cost 是 是 Lyapunov 函数, 是 system latency 的平均 - 在这道题中,由于
,所以 等价于原始 Lyapunov 优化中的虚拟队列 - 已经有其他研究证明:
- (
就是不考虑系统稳定性的情况?) 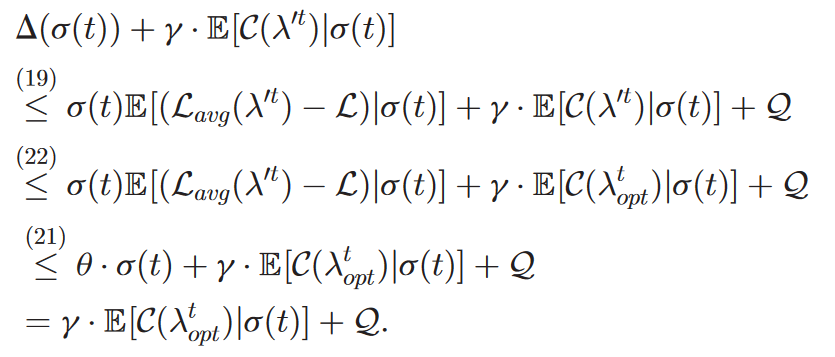
- 累加
,得: 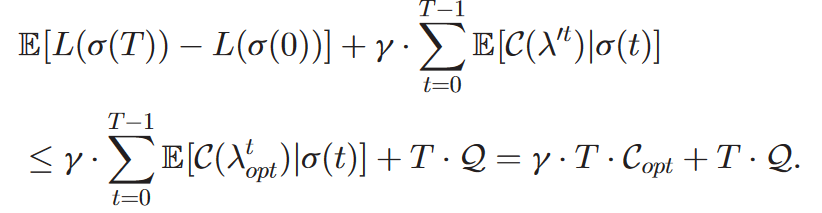
- 假设最优化问题
- 定理4:CEDC-O 算法按时间平均的累积延时(accumulated latency)是
级别的
所以,
Simulation
Settings
环境设置:(Dataset)
没什么特别的
比较对象:(Algorithm)
- Delay-Oriented
- Online-Optimal:直接求解约束规划问题
,但是由于原约束涉及到无穷的情形,所以将约束条件替换为: 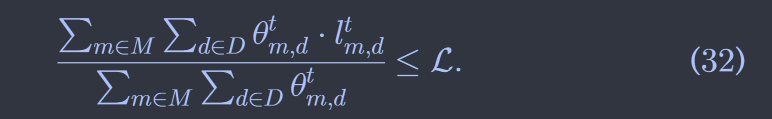
- IPEDC:在最小化 cost 的前提下覆盖临近的用户。但是在我们得情形中有些用户可能不会被覆盖,所以我们修改了原始了 IPEDC 算法,转而在不违反延时限制(即式 32)的前提下覆盖尽可能多的用户。
- Maximum Revenue:最大化
( )
参数设置(Parameter)

从 set #1 开始,每次改变一个参数(固定其它 6 个)
评价指标

Performance Comparison
对于 System Cost:
单个 time slot 的 cost:CEDC-O 比 OO 高 8.60%,并不是很显著,因为 OO 也求了 CEDC 问题的最优解。
但是在 2/3 的time slots 中,CEDC-O 比 OO 更优,说明 CEDC-O 相比 OO 而言有总体的优势(overall advantage)。
其它几幅图感觉没什么特殊的?
Impact of Edge Server Number & Data Number & ……
感觉很详细地介绍了每一个参数地变化会导致算法地结果会产生什么变化
基本上覆盖了所有情况(共
Threats to Validity【效度】
这一部分论证了算法 CEDC-O 的 有效性验证 是否可靠。
Construct Validity
主要威胁结构有效性的是用于比较的四种方法。由于 CEDC 问题在 EC 环境中的新颖性,用于比较的四种方法(DO、OO、IPEDC、MR)可能不足以全面评估 CEDC-O 算法。
为了尽量减少这种威胁,我们:
- 通过将 (32) 包含到它们的实现中来增强了 IPEDC 和 MR
- 更改了七个参数,以模拟各种 CEDC 场景 —— 演示参数更改如何影响CEDC-O的性能
External Validity【普适性】
主要的外部有效性威胁是 CEDC-O 是否可以被推广应用于 EC 环境中的其他 CEDC 场景。
为了解决这个威胁,这篇论文:
- 用通用的方式测量了 CEDC-O 的性能。具体来说,通过数据单元的数量来表示数据大小和缓存空间,并通过跳数来表示数据检索延迟。这样,评估结果可以用任意的具体模型来解释。
- 采用了被广泛使用的真实世界的数据集
- 改变了 7 个变量来模拟不同大小、不同复杂度的 CEDC 问题
通过以上方法保证了评估的代表性和综合性(the representativeness and comprehensiveness of the evaluation)。
Motivation:在这篇论文之前的工作中,如果一个用户在覆盖他的 edge server 中没有找到所需要的 data,就只能从 cloud 中找 data.
CEDC-O 采用李雅普诺夫优化
最近有论文用李雅普诺夫优化确定边缘数据完整性
在周五的报告中,可以不详细介绍李亚普优化的具体实现和理论证明,但是最好介绍一下李亚普优化有哪些应用。
一般用于:在稳定 A 的前提下(相对“稳定”,可以有一定牺牲,控制在一定范围),优化 B